Calculus Homework Help



  • We offer quality and prompt Calculus Homework Help


  • We can help you with any kind of Calculus assignments, from any level, including Pre-Calculus, Calculus I, II and III and Multivariate Calculus


  • Our service is convenient, confidential and efficient. We provide calculus help for you.


  • Our rate starts $25/hour. We provide a free quote in hours. Quick turnaround!


  • E-mail your problems for a free quote


For you guys taking calculus classes we have a lot to offer (see the topics). We know how challenging the transition from high school to college can be. There's no need to struggle with incomplete study material. That's why we offer our math assistance. We can make your life easier with our calculus homework assistance.


Submit your calculus problems for a free quote and we will be back shortly with a estimate of the cost. It costs you NOTHING to find out how much it would be to solve your problems. See a sample of our work.


We provide a quality problem solving service on the following calculus topics:

  • Functions
    • Polynomials
    • Rational Functions
    • Logarithms
    • Exponentials
    • Trigonometric

  • Limits
    • Direct Substitution Property
    • Undetermined Forms
    • Trigonometric Limits
    • Factorization
    • Side Limits
    • L'Hopital Rule

  • Continuity
    • Connection with limits
    • Algebraic Properties
    • Intermediate Value Theorem

  • Derivatives
    • Tangent Line
    • Product Rule
    • Quotient Rule
    • Chain Rule
    • Related Rates
    • Mean Value Theorem
    • Maximum and Minimum values

  • Integrals
    • Anti-derivatives
    • Fundamental Theorem of Calculus
    • Substitutions and change of variables
    • Partial Fractions
    • Improper Integrals

  • Series
    • Positive Series
    • Convergence criteria
    • Alternating Series


We know how it feels to deal with hard calculus problems. With our help, you'll get that extra edge you need! No need to sweat with poorly explained problems from the books. We can provide solutions that suit your own needs. E-mail us your calculus problems and we will send a free quote in hours. See some samples of our work.

Contact Us!


Why we can help with your Calculus?

Year of Experience

We have been online for more than 10 years, we have worked with thousands of customers who have been able to appreciate the quality of our work

Calculus Expertise

Calculus can be a tough subject, and our tutors are the right experts to help you with your homework or anything academic related with Calculus

Step-by-Step Solutions

Our tutors provide detailed, step-by-step solutions, and we put a lot of care in double checking our calculations

Free Quote

You can e-mail us your problems 24x7. We will send a free quote ASAP

Very Competitive Prices

We try to accommodate to all budgets. No job is to big or too small with us. We make our best to accommodate to our customers' needs

We take pride of our work

We do our work with care. We are experts and we take pride in what we do. Our main objective is our customers' complete satisfaction. We take great care in paying attention to all the requirements and details, with the purpose of fulfilling work of the highest quality

and more...

Prices

Prices start at $25 per hour, depending on the complexity of the work and the turnaround time

Contact Us

You can e-mail us your problems for a free quote.


SAMPLE CALCULUS PROBLEMS

Problem 1. Find

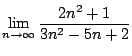
$\displaystyle \lim_{n\rightarrow \infty} \frac{2n^2+1}{3n^2-5n+2}$

Solution.

The problem presents the typical case of a quotient of two quantities that go to infinity. In fact, $ 2n^2+1$ and $ 3n^2-5n+2$ both approach to infinity as $ n\rightarrow\infty$ . Which means that the quotient

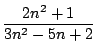
$\displaystyle \frac{2n^2+1}{3n^2-5n+2}$

is an undetermined form. Somehow we have to cancel the "bad" part, if possible. Notice that since both $ 2n^2+1$ and $ 3n^2-5n+2$ are big, there's a chance for cancelation, so the quotient could be finite.

The trick in this case is to divide by the highest power on the expression (from both numerator and denominator). In this case we will divide both numerator and denominator by $ n^2$ . We get

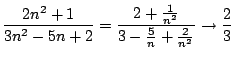
$\displaystyle \frac{2n^2+1}{3n^2-5n+2}= \frac{2+\frac{1}{n^2}}{ 3-\frac{5}{n}+\frac{2}{n^2} }\rightarrow \frac{2}{3}$

as $ n\rightarrow\infty$ because $ \frac{1}{n^2}\rightarrow 0$ , $ \frac{5}{n}\rightarrow 0$ and $ \frac{2}{n^2} \rightarrow 0$ as $ n\rightarrow\infty$ .

This trick is applied in general for this type of expressions. $ \Box$



Problem 2. Find $ \frac{dy}{dx}$ and $ \frac{d^2 y}{dx^2}$ if

$\displaystyle x^{2/3}+y^{2/3}=a^{2/3}, \qquad a>0 $


Solution. Let's differentiate both sides of the equality. Let's recall that we are assuming that $ y=y(x)$ . That means that the equation gives us a way to solve $ y$ as a function of $ x$ , but we still don't know how to express that function. That assumption requires further justification (meaning, it's not always granted), but we'll take it for granted. So, since $ y=y(x)$ we get using the chain rule:

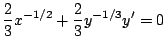
$\displaystyle \frac{2}{3} x^{-1/2}+\frac{2}{3} y^{-1/3} y'=0 $

where $ y'\equiv \frac{dy}{dx}$ . The 0 on the right hand side comes from differentiating the constant $ a^{2/3}$ . We multiply the equation by $ 3/2$ and we get

$\displaystyle x^{-1/2}+ y^{-1/3} y'=0 $

which means that

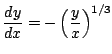
$\displaystyle \frac{dy}{dx} = -\left(\frac{y}{x}\right)^{1/3} $

Let's get $ y''$ . From the last equation we obtain easily that

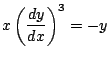
$\displaystyle x\left(\frac{dy}{dx}\right)^3=-y $

and now we differentiate this again with respect to $ x$ to get:

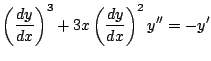
$\displaystyle \left(\frac{dy}{dx}\right)^3+3x\left(\frac{dy}{dx}\right)^2 y''=-y' $

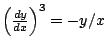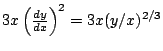But $ \left(\frac{dy}{dx}\right)^3=-y/x$ and $ 3x\left(\frac{dy}{dx}\right)^2=3x(y/x)^{2/3}$ . We know put all the elements together:

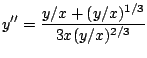
$\displaystyle y''=\frac{y/x+(y/x)^{1/3}}{3x(y/x)^{2/3}} $

and now we simplify the right hand side of the last equation

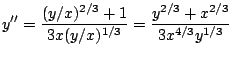
$\displaystyle y''=\frac{(y/x)^{2/3}+1}{3x(y/x)^{1/3}}=\frac{y^{2/3}+x^{2/3}}{3x^{4/3}y^{1/3}} $

But by definition: $ x^{2/3}+y^{2/3}=a^{2/3}$ , so we replace this into the previous equation:

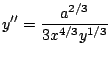
$\displaystyle y''=\frac{a^{2/3}}{3x^{4/3}y^{1/3}} $

which gives the final answer.$ \Box$