Operations Management Help
|
Operations Management is the corner stone of the real-world applications in the management science. It brings many powerful tools altogether, blending several Statistics and Optimization techniques. We offer homework assistance in several OM topics.
Commonly, the textbooks come mostly with the answers to some of the problems, but they don't show detailed, step-by-step solutions. Our goal is to provide you with clear and well explained solutions to your problems. Our turnaround time is 24-48 depending on the request.
We can work with various software programs, such as POM - QM, The Management Scientist, Excel, Crystal Ball, Excel OM, LINDO, GAMS, Matlab, etc.
Submit your Operations Management homework problems for a free quote and we will be back shortly with an estimate of the cost. It costs you NOTHING to find out how much it would be to solve your problems. See a sample of our work.
We provide a quality problem solving service on the following Operations Management topics:
- Forecasting
- Moving Averages
- Exponential Smoothing
- Linear Trends
- Seasonal Components
- Statistical Process Control
- Control Charts
- X-bar, R-bar, p-bar, C-bar charts
- Process Capability
- Decision Theory
- Maximax and Maximin
- Minimax Regret
- Expected Monetary Value
- Expected Value of perfect information (EVPI)
- Expected Value of sample information (EVSI)
- Decision Trees
- Utility
- Location Strategies
- Factor Rating
- Center of Gravity
- Transportation Model
- Layout Strategy
- Fix-position layout
- Processed Oriented layout
- Office layout
- Warehouse layout
- Forecasting
- Inventory Models
- A-B-C analysis
- Economic Order Quantity (EOQ)
- Economic Production Quantity (EPQ)
- Quantity Discount Models
- One-Period Model
- Just in Time systems (JIT)
- PERT
- Single Estimate
- Triple Estimate
- Cost Crashing
- Critical Paths
- Gantt-Charts
- Aggregate Scheduling
- Demand Chase
- Mixed Strategy
- Material Requirement Planning (MRP)
- Bills of material
- Lot-for-lot
- Linear Programming
- Linear Programming
- Transportation Problems
- Transshipment
- Integer Programming
- Assignment Problems
- Network Problems
- Waiting-Line models
- Queues
- Single-Channel and Multi-Channel models
- Simulation
- Simulations in Excel
- Monte Carlo Methods
Why we can help with your Operations Management?
Year of Experience
We have been online for more than 10 years, we have worked with thousands of customers who have been able to appreciate the quality of our work
Operations Management Expertise
Operations Management can be a tough subject due to the many concepts that need to be mastered and the number of formulas a student need to master in order to be in good standing. Our tutors are the right experts to help you with your homework or anything academic related with Operations Management
Step-by-Step Solutions
Our tutors provide detailed, step-by-step solutions, and we put a lot of care in double checking our calculations
Free Quote
You can e-mail us your problems 24x7. We will send a free quote ASAP
Very Competitive Prices
We try to accommodate to all budgets. No job is too big or too small with us. We make our best to accommodate to our customers' needs
We take pride of our work
We do our work with care. We are experts and we take pride in what we do. Our main objective is our customers' complete satisfaction. We take great care in paying attention to all the requirements and details, with the purpose of fulfilling work of the highest quality
and more...
Sample Operations Management Problems
Question: The costs of placing an order is $150. It is estimated that 1,000 units will be used in the next 12 months. The carrying cost per unit per month is $2.50.
a. Compute the optimum order size
b. Now suppose that the company could lower the ordering cost to $50; the cost of the effort to accomplish this change is $1,000. Assume the product will be sold only for the next two years. Compute the new optimal order quantity if the lower ordering cost were implemented, and determine if the company should invest $1,000 in the ordering-cost reduction program.
Solution: (a) The following is obtained:
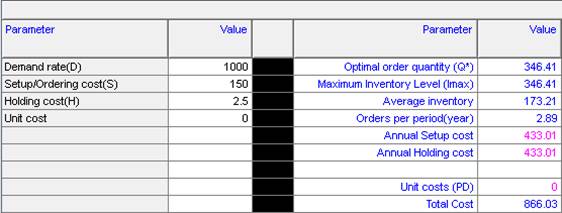
Hence, the optimal order quantity is
\[EOQ=\sqrt{\frac{2DS}{H}}=\sqrt{\frac{2\times 1000\times 150}{2.5}}=346.41\]
The total inventory cost is TC = $866.03.
(b) IF the setup cost was reduced to $50, we would get
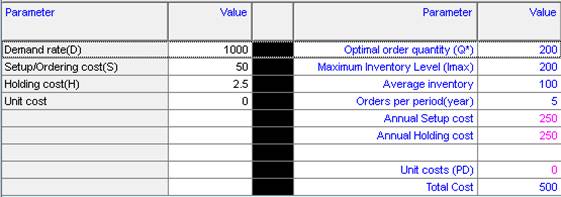
In this case, the optimal order quantity is EOQ = 200, and the total inventory cost is $500. The savings in cost for 2 years operation are (866.03 – 500)*2 =$732.06, which is less than $1000 (the cost of reducing the setup cost), and hence, the ordering-cost reduction program should not be pursued.
Question: A logistics specialist for Wiethoff Inc. must distribute cases of parts from 3 factories to 3 assembly plants. The monthly supplies and demands, along with the per-case transportation costs are:

What are the total monthly transportation costs for the optimal solution?
Solution: We have 9 variables \({{x}_{ij}}\), where \({{x}_{ij}}\) represents the amount that is sent from factory![]() to assembly plant
to assembly plant![]() . For convenience of notation, we name the factories A, B and C as 1, 2 and 3.
. For convenience of notation, we name the factories A, B and C as 1, 2 and 3.
The problem is written as
\[\begin{align} & \text{Minimize }\sum\limits_{i,j=1}^{3}{{{C}_{ij}}{{X}_{ij}}} \\ & \text{subject to }{{X}_{11}}+{{X}_{12}}+{{X}_{13}}\le 200 \\ & \text{ }{{X}_{21}}+{{X}_{22}}+{{X}_{23}}\le 400 \\ & \text{ }{{X}_{31}}+{{X}_{32}}+{{X}_{33}}\le 200 \\ & \text{ }{{X}_{11}}+{{X}_{21}}+{{X}_{31}}=120 \\ & \text{ }{{X}_{12}}+{{X}_{22}}+{{X}_{32}}=620 \\ & \text{ }{{X}_{13}}+{{X}_{23}}+{{X}_{33}}=60 \\ & \text{ }{{X}_{ij}}\ge 0 \\ \end{align}\]
We know solve this problem using Excel’s solver. The output is shown below:
|
Plants |
Variables |
||||||||
|
1 |
2 |
3 |
1 |
2 |
3 | ||||
|
A |
5 |
9 |
16 |
A |
0 |
200 |
0 | ||
|
Factories |
B |
1 |
2 |
6 |
B |
0 |
400 |
0 | |
|
C |
2 |
8 |
7 |
C |
120 |
20 |
60 | ||
|
1 |
2 |
3 |
|||||||
|
\({{\mathbf{c}}_{ij}}{{\mathbf{x}}_{ij}}\) |
1 |
0 |
1800 |
0 |
|||||
|
2 |
0 |
800 |
0 |
Objective |
3420 |
||||
|
3 |
240 |
160 |
420 |
||||||
|
Restrictions |
|||||||||
|
Supply |
|||||||||
|
Slack 1 |
0 |
200 |
|||||||
|
Slack 2 |
0 |
400 |
|||||||
|
Slack 3 |
0 |
200 |
|||||||
|
Demand |
|||||||||
|
Slack 4 |
0 |
||||||||
|
Slack 5 |
0 |
||||||||
|
Slack 6 |
0 |
This means that 120 cases of parts are sent from factory C to Plant 1. The total monthly transportation costs are $3,420.
Operations Management Blog
Excel OM example for Economic Order Quantity.
Check out how to deal with some waiting lines examples.
How to compute the capability index.
See this example of a PERT case study.
How to work Linear Programming problems using LINDO.
Check out these PERT case study with crashing using the Management Scientist.
Find out how to use the EOQ formulas to find the optimal inventory levels.
