Statistics Help Online


We offer you quality and prompt Statistics Help Online.

We can solve Stats Problems for you so you can be sure to have the right solution.

We provide you with Stats Help for any kind of statistics subjects, including Elementary Statistics, Business Statistics, Biostatistics, Probabilities, Advanced Statistics, etc.

Our service is efficient and convenient. We can solve Stats problems for you, with results guaranteed.

Get help with your EXCEL, SPSS, SAS, STATA, JMP and MINITAB assignments and projects.

Our rate starts $35/hour. We will send you a Free Quote in hours. Quick turnaround!


Statistics is one of the most important tools for your professional career. Make your life easier by getting the right help. Think how important it is to pass and get a good grade on that statistics class that is giving you a headache. Don't wait until is too late. You deserve to get the best possible help NOW.


Submit your problems for a free quote and we will be back shortly (a couple of hours max). It costs you NOTHING to find out how much it would cost to solve your problems. See a sample of our work.






We provide a quality problem solving service on the following stats topics:

  • Probability
    • Basic Concepts: Sample Space, Events.
    • Densities and Distributions.

  • Descriptive statistics.
    • Descriptive Analysis of data.
    • Graphs and charts.

  • Inferential Statistics
    • Means, variances, populations, samples.
    • Intervals of Confidence.
    • Z-test, T-test and F-tests.
    • Hypothesis Testing.
    • ANOVA.
    • Correlation.
    • Linear and non-linear regression.

  • Non-parametric Statistics.
    • Sign Test.
    • Wilkinson Tests.
    • Kruskal-Wallis Test.
    • Spearman Correlation Coefficient.


Our team is highly experienced in SPSS, Minitab, EXCEL and the majority of the statistical software packages out there. Request your free quote.. We a have a satisfaction guarantee policy. If you're not satisfied, we'll refund you. Please see our terms of service for more information about the satisfaction guaranteed policy. See also a sample of our work.

Contact Us!


Why we can help with your Stats?

Experience

We have successfully helped customers online for more than 10 years now

Statistics Expertise

We can do handle any type of statistics analyis/homework/questions. Our tutors have real expertise, and big majority of our customers are returning customers

Step-by-Step Solutions

We provide detailed, step-by-step solutions, and we strive to provide exactly what our customers want.

Free Quote

E-mail us your homework problems, we will review them and promptly come back to you with a free quote

Very Competitive Prices

We strive to provide the best possible prices for our services

We take pride of our work

Our tutors take pride on the work we do. We diligenty do work for our customers, and put great attention to details striving to always provide a great final product

and more...

Prices

Prices start at $25 per hour, depending on the complexity of the work and the turnaround time

Contact Us

You can e-mail us your problems for a free quote.


Sample Problem. The time it takes an international telephone operator to place an overseas phone call is normally distributed with mean 45 seconds and standard deviation 10 seconds.


a. What is the probability that my call will go through in less than 1 minute?


b. What is the probability that I will get through in less than 40 seconds?


c. What is the probability that I will have to wait more than 70 seconds for my call to go through?


Solution:


a. First thing is, let $X$ be the time it takes to the telephone operator to place an overseas phone call. The probability we are looking for is


\begin{displaymath}\Pr (X<60)\end{displaymath}

In order to compute this probability, we need to normalize $X$ in the following way. We know that $Z=\frac{X-\mu }{\sigma }$ has standard normal distribution, so we compute


\begin{displaymath} \Pr (X<60)=\Pr \left( {\frac{X-\mu }{\sigma }<\frac{60-\mu }... ... \left( {\frac{X-45}{10}<\frac{60-45}{10}} \right)=\Pr(Z<1.5)\end{displaymath}


\begin{displaymath} \Phi (1.5)=0.933193 \end{displaymath}

(notice that since the mean is given in seconds, we have to write 1 minute as 60 seconds)


b. Same as before, let $X$ be the time it takes to the telephone operator to place an overseas phone call. The probability we are looking for is


\begin{displaymath} \Pr (X<40) \end{displaymath}

In order to compute this probability, we need to normalize $X$ in the same way we did before. We know that $Z=\frac{X-\mu }{\sigma }$ has standard normal distribution, so we compute


\begin{displaymath} \Pr (X<40)=\Pr \left( {\frac{X-\mu }{\sigma }<\frac{40-\mu }... ...\left( {\frac{X-45}{10}<\frac{40-45}{10}} \right)=\Pr (Z<-0.5) \end{displaymath}


\begin{displaymath} \Phi (-0.5)=0.308538\end{displaymath}

c. $X$ is the time it takes to the telephone operator to place an overseas phone call. The probability we are looking for is equal to


\begin{displaymath} \Pr (X>70)=1-\Pr (X\le 70) \end{displaymath}

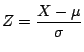As before, we need to normalize $X$. We get that $Z=\displaystyle\frac{X-\mu }{\sigma }$ has standard normal distribution, and we compute


\begin{displaymath} \Pr (X\le 70)=\Pr \left( {\frac{X-\mu }{\sigma }\le \frac{70... ...eft( {\frac{X-45}{10}<\frac{70-45}{10}}\right)=\Pr (Z\le 2.5) \end{displaymath}


\begin{displaymath}\Phi(2.5)=0.99379\end{displaymath}

and therefore $\Pr (X>70)=1-\Pr (X\le 70)=0.00621$.

Statistics Help Blog

Learn how to use Excel to Run a t-test on the context of a Case Study of Inferential Statistics

Excel can be used to solve different types of correlation and regression problems. Check it out.

Regression analysis with Excel can also be used to work on Time series analysis problems.

Excel can be used for the majority of elementary inferential statistics procedures, including a test for two samples.

Regression with Excel can be used to estimate stock prices and beta coefficients.

One-Way ANOVA, along with two-samples t-test and regression are among the tests that Excel can help you with.

Learn About Two-Way Chi-Square test Using Excel.

Working with Examples of Normal Distribution probability calculations.