Statistics Answers


  • MGT offers quality and prompt Statistics Homework Answers, with detailed solutions.


  • We can solve Statistics Homework problems for you, and provide you with the homework answers you are looking for


  • We can provide you with any kind of Statistics homework solutions


  • Our service is convenient, proven and confidential. We can solve all kinds of homework problems for you, with guaranteed results.


  • Our rate starts $25/hour. We will send you a free quote in hours. Quick turnaround!


One thing students will always talk about is their Stats homework. Either it is because they are lost in a class they are taking, or the teacher does not explain the concepts well, or the homeworks are too long, or the graders are too harsh. You name it.

We have heard everything. One thing we do know is that a percentage of students will need help with their Stats homework. Make your life easier by getting the right help. It is key to get helped by an expert in order to get the results that you want and deserve.


Submit your homework problems for a free quote and we will be back shortly (a couple of hours max). It costs you NOTHING to find out how much it would cost to get the answers. See a sample of our work.






We provide a quality problem solving service on the following homework topics:

  • Probability
    • Basic Concepts: Sample Space, Events.
    • Densities and Distributions.

  • Descriptive Statistics.
    • Descriptive Analysis of data.
    • Graphs and charts.

  • Inferential Statistics
    • Means, variances, populations, samples.
    • Intervals of Confidence.
    • Z-test, T-test and F-tests.
    • Hypothesis Testing.
    • ANOVA.
    • Correlation.
    • Linear and non-linear regression.

  • Non-parametric Statistics.
    • Sign Test.
    • Wilkinson Tests.
    • Kruskal-Wallis Test.
    • Spearman Correlation Coefficient.


Our team has vast experience in handling homework requests, for all kinds of subjects. We understand the need of detailed, step-by-step quality solutions to homewor problems. Request your free quote.. We a have a satisfaction guarantee policy. If you're not satisfied, we'll refund you. Please see our terms of service for more information about the satisfaction guaranteed policy. See also a sample of our work.

Contact Us!


Why we can help with your Stats?

Experience

We have successfully helped customers online for more than 10 years now

Statistics Expertise

We can do handle any type of statistics analyis/homework/questions. Our stats tutors have real expertise, and big majority of our customers are returning customers

Step-by-Step Solutions

We provide detailed, step-by-step solutions, and we strive to provide exactly what our customers want.

Free Quote

E-mail us your problems, we will review them and promptly come back to you with a free quote

Very Competitive Prices

We strive to provide the best possible prices for our services

We take pride of our work

Our tutors take pride on the work we do. We diligenty do work for our customers, and put great attention to details striving to always provide a great final product

and more...

Prices

Prices start at $25 per hour, depending on the complexity of the work and the turnaround time

Contact Us

You can e-mail us your problems for a free quote.


Sample Problem. The time it takes an international telephone operator to place an overseas phone call is normally distributed with mean 45 seconds and standard deviation 10 seconds.


a. What is the probability that my call will go through in less than 1 minute?


b. What is the probability that I will get through in less than 40 seconds?


c. What is the probability that I will have to wait more than 70 seconds for my call to go through?


Solution:


a. First thing is, let $X$ be the time it takes to the telephone operator to place an overseas phone call. The probability we are looking for is


\begin{displaymath}\Pr (X<60)\end{displaymath}

In order to compute this probability, we need to normalize $X$ in the following way. We know that $Z=\frac{X-\mu }{\sigma }$ has standard normal distribution, so we compute


\begin{displaymath} \Pr (X<60)=\Pr \left( {\frac{X-\mu }{\sigma }<\frac{60-\mu }... ... \left( {\frac{X-45}{10}<\frac{60-45}{10}} \right)=\Pr(Z<1.5)\end{displaymath}


\begin{displaymath} \Phi (1.5)=0.933193 \end{displaymath}

(notice that since the mean is given in seconds, we have to write 1 minute as 60 seconds)


b. Same as before, let $X$ be the time it takes to the telephone operator to place an overseas phone call. The probability we are looking for is


\begin{displaymath} \Pr (X<40) \end{displaymath}

In order to compute this probability, we need to normalize $X$ in the same way we did before. We know that $Z=\frac{X-\mu }{\sigma }$ has standard normal distribution, so we compute


\begin{displaymath} \Pr (X<40)=\Pr \left( {\frac{X-\mu }{\sigma }<\frac{40-\mu }... ...\left( {\frac{X-45}{10}<\frac{40-45}{10}} \right)=\Pr (Z<-0.5) \end{displaymath}


\begin{displaymath} \Phi (-0.5)=0.308538\end{displaymath}

c. $X$ is the time it takes to the telephone operator to place an overseas phone call. The probability we are looking for is equal to


\begin{displaymath} \Pr (X>70)=1-\Pr (X\le 70) \end{displaymath}

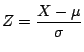As before, we need to normalize $X$. We get that $Z=\displaystyle\frac{X-\mu }{\sigma }$ has standard normal distribution, and we compute


\begin{displaymath} \Pr (X\le 70)=\Pr \left( {\frac{X-\mu }{\sigma }\le \frac{70... ...eft( {\frac{X-45}{10}<\frac{70-45}{10}}\right)=\Pr (Z\le 2.5) \end{displaymath}


\begin{displaymath}\Phi(2.5)=0.99379\end{displaymath}

and therefore $\Pr (X>70)=1-\Pr (X\le 70)=0.00621$.